Plotting functions

[Nelson-numerical-software]

Compatible plotting functions will come before end of the year (2022) in Nelson
Here some preview:

x = repmat(linspace(-1,1), [100, 1]);
y = x';
z = exp(-x .^2 - y .^2);
f1 = figure(1);
imagesc(z);

x = linspace(-1, 1);
y = cos(5 * pi * x);
f2 = figure(2);
plot(x, y, 'r-')

[Nelson-numerical-software]

f = figure();
x = repmat(linspace(-1, 1), [100,1]);
y = x';
r = x .^ 2 + y  .^ 2;
z = exp(-r * 3) .* cos(5*r);
c = r;
surf(x, y, z, c);
view(3);
title('Made with love with Nelson');

[Nelson-numerical-software]

f = figure();
t = 0:pi/500:40*pi;
xt = (3 + cos(sqrt(32)*t)).*cos(t);
yt = sin(sqrt(32) * t);
zt = (3 + cos(sqrt(32)*t)).*sin(t);

plot3(xt,yt,zt)
xlabel('x(t)')
ylabel('y(t)')
zlabel('z(t)')

[Nelson-numerical-software]

f = figure()
subplot(2,2,1)
x = repmat(linspace(-1, 1), [100,1]); y = x';
z = exp(x .^2 - y .^2);
image(z)

subplot(2,2,2)
t = 0:pi/500:40*pi;
xt = (3 + cos(sqrt(32)*t)).*cos(t);
yt = sin(sqrt(32) * t);
zt = (3 + cos(sqrt(32)*t)).*sin(t);
plot3(xt,yt,zt)
xlabel('x(t)')
ylabel('y(t)')
zlabel('z(t)')

subplot(2,2,3)
H = plot(rand(5));

subplot(2,2,4)
x = linspace(-2*pi,2*pi);
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2)

[Nelson-numerical-software]

[Nelson-numerical-software]

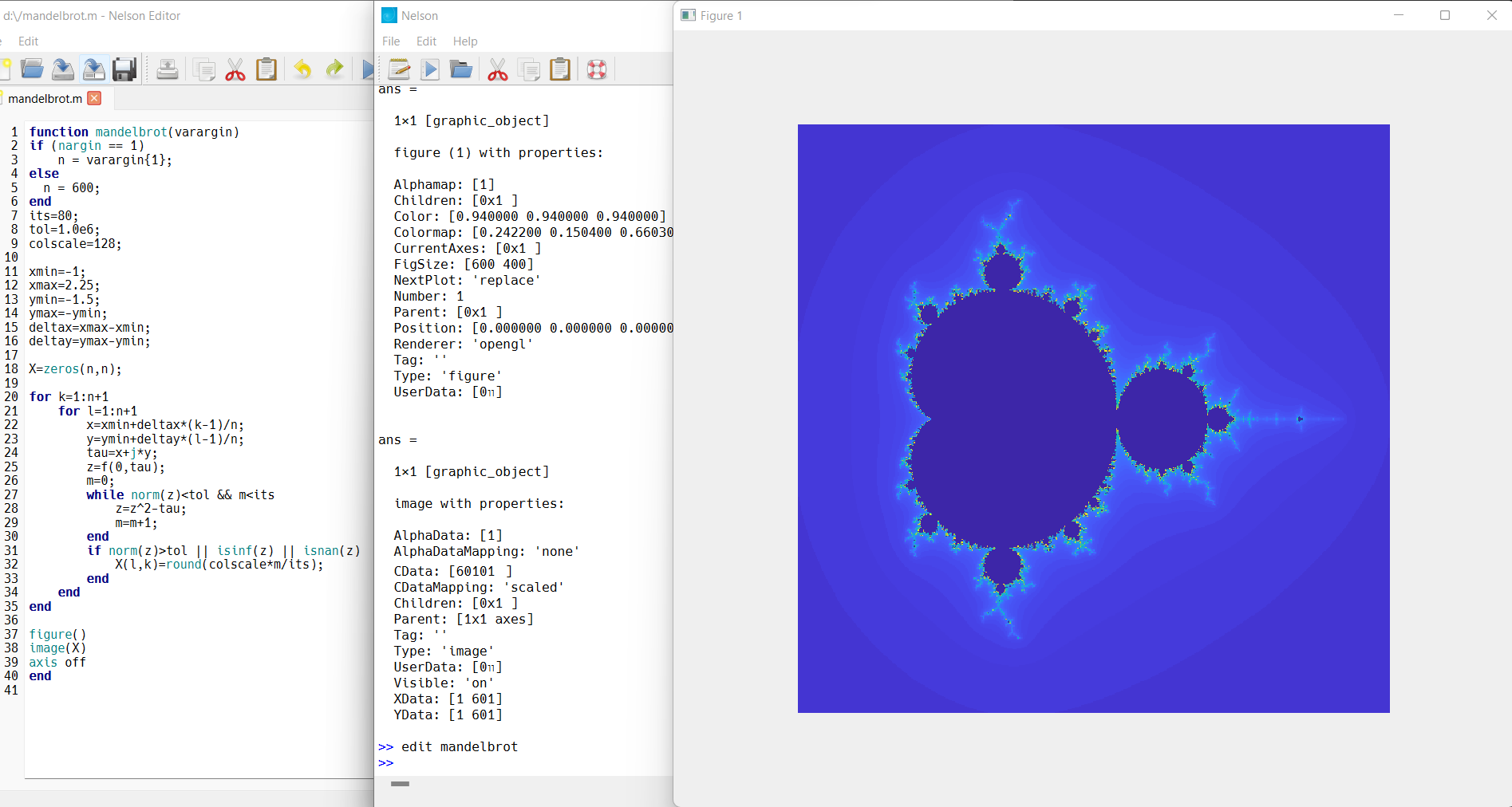
Mandelbrot's fractal

function mandelbrot(varargin)
if (nargin == 1)
    n = varargin{1};
else
  n = 600;
end
its=80;
tol=1.0e6;
colscale=128;

xmin=-1;
xmax=2.25;
ymin=-1.5;
ymax=-ymin;
deltax=xmax-xmin;
deltay=ymax-ymin;

X=zeros(n,n);

for k=1:n+1
    for l=1:n+1
        x=xmin+deltax*(k-1)/n;
        y=ymin+deltay*(l-1)/n;
        tau=x+j*y;
        z=f(0,tau);
        m=0;
        while norm(z)<tol && m<its
            z=z^2-tau;
            m=m+1;
        end
        if norm(z)>tol || isinf(z) || isnan(z)
            X(l,k)=round(colscale*m/its);
        end
    end
end

figure()
image(X)
axis off
end

[Nelson-numerical-software]

Faster mandelbrot using vectorization (x100)

tic()
step = 0.01; 
dx = step; 
x1 = -2;
x2 = 2;
dy = step;
y1 = -1.5;
y2 = 1.5;
x = x1:dx:x2;
y = y1:dy:y2;
[X,Y] = meshgrid(x,y);
c = X + 1i*Y;
R = 10;
n = 100;
z = zeros(size(c));
for nc=1:n
    z=z .^ 2 + c; 
end
I = abs(z)<R;
imagesc(x,y,I);
toc()